Yes, it’s that time of the year when everyone will start talking turkey. Whether it's for a lovely Thanksgiving dinner or a joyous Christmas meal, turkey remains a firm favourite.

Have you considered smoking a whole turkey though? Not only does it look stunning, but it will probably be a surprise for everyone. I am sure that none of your guests had ever seen or tasted a whole smoked turkey.
With a really handy smoker, you too can create an alternative Christmas meal with a twist. The best part is, that even if you don’t eat up the whole turkey, you have plenty of leftovers. You can create leftover turkey sandwiches, casseroles and much more. However if you don't want to smoke a whole turkey that's fine too, check out this smoked turkey legs recipe for a smaller cut.
whole smoked turkey with Char-Broil
Is it even possible to smoke a whole turkey? The answer is yes - with the correct smoker at home you can! Let the gadget do all the work for you. All you’ll need to do is to brine it first and then place it in the smoker until it’s ready. You can purchase a smoker from Char-Boil to spice up your upcoming holidays.
Luckily, Char-Broil offers so many products that can fit any need you might have in terms of smoking. They have a whole line of BBQ smokers, electric smokers, Oklahoma Joe's® Smoker and Oilless Fryers.

The Big Easy® Smoker Roaster/Fryer & Grill
Of course, the one I used for this whole smoked turkey recipe was The Big Easy® Smoker Roaster/Fryer & Grill. It lets you smoke, roast, fry and grill all at once. It’s very impressive that one device can have so many functions and features.
With the TRU-Infrared technology, my whole smoked turkey was evenly cooked and juicy all the way. Did I mention that this whole process was oilless? The Big Easy® series are oil-less fryers and it makes the process really convenient and easy.
All you have to do is put some wood chips in the side panel, push the button and let it smoke. Once it’s done, you just need to remove the grease tray. Gone are the days when cleaning grease off the kitchen counters and ovens took forever.
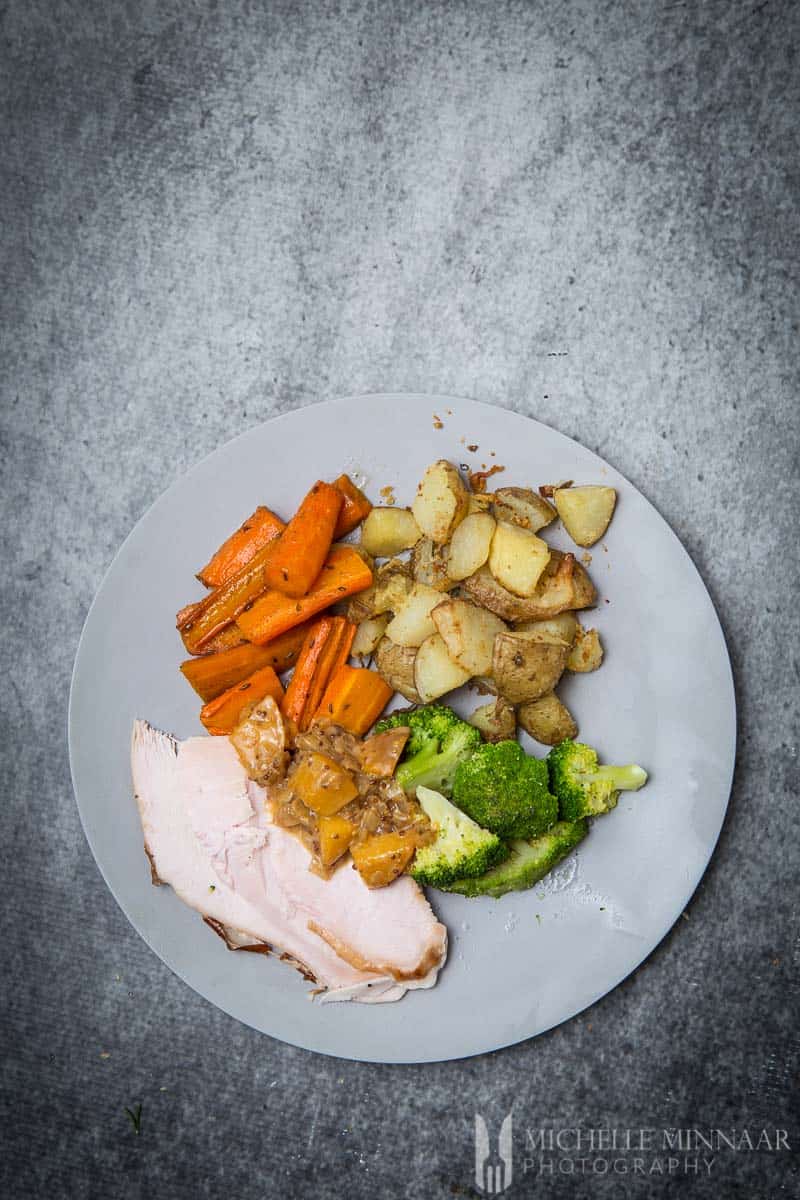
Lastly, the best part is that The Big Easy® Smoker Roaster/Fryer & Grill is very versatile when it comes to meat. You don’t necessarily have to make a whole smoked turkey. Chicken, quail, beef, lamb or even fish are also some excellent candidates for smoking.
You can put any cuts of meat up to 25 pounds in a roasting basket and easily get it out. Also, along with the different cuts of meat, you can also use vegetables.
I would recommend smoking a corn cob and serving it with some butter. This device is definitely a huge asset for the upcoming holidays.
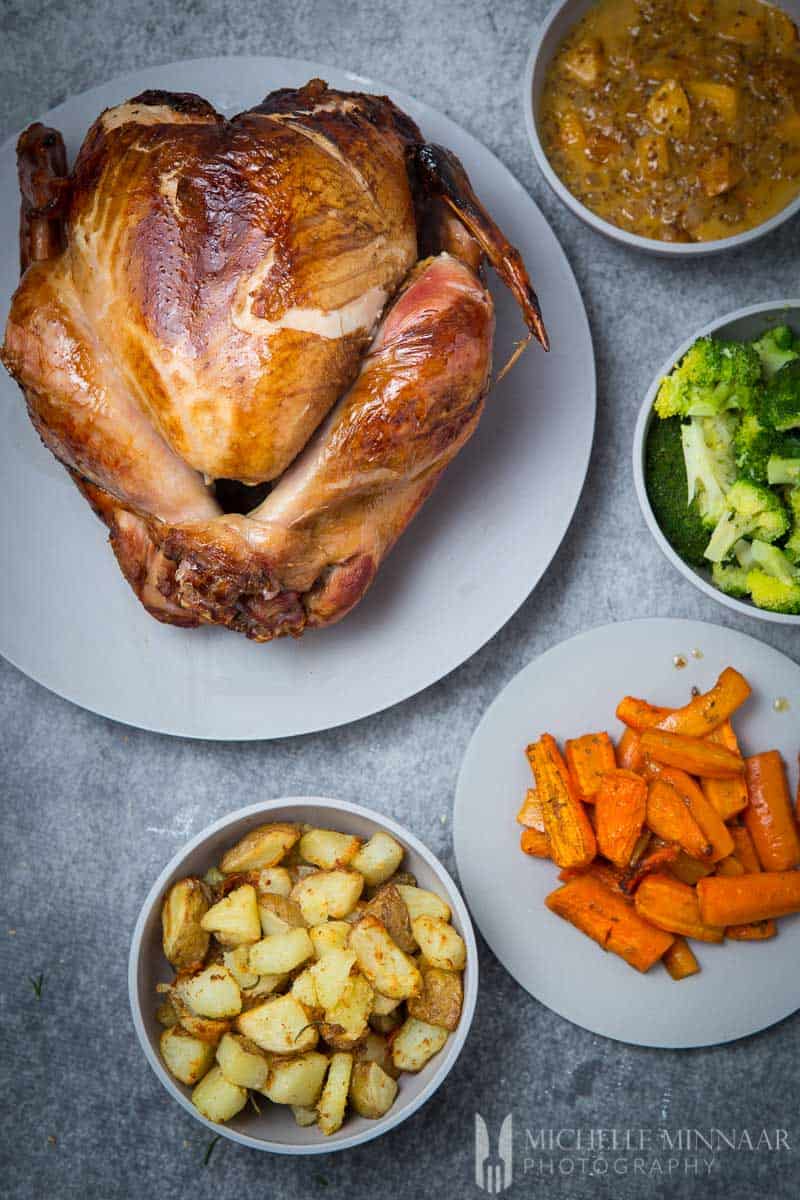
preparation
Have any of you ever had any experience of smoking an entire bird? If, by some coincidence, you do then you’ll probably know that brining can be slightly complicated. Especially, if you lack the proper equipment to brine the whole thing in.
Now remember, the turkey is a rather large bird - it’s usually double the size of a chicken. So here comes the next question - where will you brine the turkey once you’ve bought one?
Would you like to save this?
Unfortunately for me, I only figured this out once I started with the process. It was then I realised I had no way of brining this whole thing properly. Some people brine their whole turkey in the kitchen sink.
This, of course, is only possible when the kitchen sink is deep enough. Also, you won’t be able to use the kitchen sink for a while once it has the huge bird in it.
In order to make things a lot tidier and more convenient, I bought a cooler box. Good thinking, right? The cooler box will let you move the whole turkey around, so it doesn’t necessarily have to clutter up your kitchen.
Fill it up with the brine and keep it chilled for 24 hours. Plus, it’s cheap and you can reuse the cooler for storage in the summer.

how to smoke
With the smoker in place, it will do the job for you. All you’ll need to do is to decide what type of woodchips you would like to use. Whether it be a fruitier type of wood for milder smoky flavours or a heavy woodchip for rich intense flavours. You can find out more about the effect different types of woodchips in my hot smoked salmon recipe.
I used apple woodchips for a mild and subtle smoky flavour in the background. Altogether, the whole smoked turkey was in the smoker for 4.5 hours. Remember to turn your turkey around for even cooking.
When the skins starts to turn a golden brown colour, cover it with some aluminum foil. This will prevent the turkey skin from burning and will give it a nice crunch.

sides
This dish is very easy to complement with side dishes. I roasted some carrots and potatoes. Roasting sweet potatoes with some thyme is also a classic. Also, to add some greens to the entire meal, why not include green beans or broccoli?
Instead of cranberry or lingonberry jelly, I made a peach and mustard sauce to go with the meat. You'll have to wait for the recipe though! As expected, the smoked turkey went down a storm and was one very memorable meal with lovely friends. If you're looking for a fruity twist to this dish, why not try this beautiful Blueberry Chutney?

Other similar recipes you might enjoy are some ribs and smoked chicken. How do you prepare the perfect turkey?
Print📖 Recipe

Whole Smoked Turkey
- Total Time: 5 hours 30 minutes
- Yield: 10 1x
Description
A whole smoked turkey is something everyone should try at least once. Whether it be during a weekend or during some celebrations. You'll need a smoker and nice big turkey. Pair with roasted vegetables such as potatoes, broccoli or carrots. It'll be hard to go back to the plain roasted stuff after you had one bite...
Instructions
- If you bought a frozen turkey, you need to thaw it first. It would take approximately 66 hours in the fridge and 22 hours in a cool room to thaw.
- For best results, the turkey needs brining. I used a cooler box to store the turkey in and then prepared enough brine to cover the turkey, which took a while! Here’s the basic recipe.
- Keep the turkey chilled in the brine in the cooler box with ice packs. After 24 hours the turkey is ready for the smoker.
- Preheat the Char-Broil Big Easy Smoker on the High setting and fill the smoking box with wood chips.
- Wait for 10 minutes until the chips begin to smoke, then change the heat setting to Low.
- Place the turkey breast side up in the basket. Place the basket inside the smoker.
- Close lid and cook until the turkey’s internal temperature is 74°C (165°F). This takes about 4 hours and 30 minutes.
- For best results, check on the turkey every 30 minutes and preferably turn it around for even cooking. If the skin is browned and crisp before it’s properly cooked, cover the bird with foil to prevent the skin from burning.
- Remove the turkey from the smoker and let it rest for about 15 minutes before carving.
Notes
- Because of the temperature discrepancy between the top and bottom area inside the smoker, you need to turn the turkey upside down every now and then. That way, both ends will get evenly cooked.
- Refrain from saucing the turkey while it’s in the smoker. Wait until it’s cooked and finish with a luscious sauce under the grill or on the barbecue. A lot less mess and no burning!
- Prep Time: 60 minutes
- Cook Time: 270 minutes
- Category: main course
- Cuisine: American
Nutrition
- Serving Size: 1 serving
- Calories: 765
- Sodium: 315 mg
- Fat: 22.5 g
- Saturated Fat: 7.4 g
- Protein: 131.8 g
- Cholesterol: 341 mg
save the recipe to your pinterest board

P.S. This is a sponsored post.





Maria P
never tried to roast a whole turkey... but turkey leg is perfect with smoked ham, a bit of mustard, salt and peper
michelle
sounds delicious
Tracey Anderson
I usually stuff with garlic and thyme stuffing and baste in a lemon and herb butter 🙂
michelle
sounds delicious
Helen Hames
Butter under the skin then bacon on top hmmmm
michelle
hmmm indeed
Miss Tracy Hanson
This year we want to try it wth a rub of garlic, cumin, chili powder, ground cor roast your turkey with a rub of garlic, chili ground coriander and crushed red pepper. But last year's lemon and orange zest rub went down a storm.
michelle
ooo I hope it all works out for you guys this year 🙂
Amanda Botterill
i cook it breast side down for half of the time
michelle
thanks for sharing Amanda
Craig AUstin
With bacon and duck fat
michelle
never thought of using duck fat! thanks for the tip Craig
Simone Griffin
My dad always prepares and cooks the turkey
michelle
nice!
Eve H Ogden
Slow cooker yummy
michelle
nice!
Lia Burns
Plenty of basting, I cover with butter and sprinkle some miced herbs over it x
michelle
love the addition of herbs on top 🙂
Sarah Revill
I rub butter under the skin and the meat is always so tender.
michelle
clever!!!!
caroline tokes
Plenty of basting to give it moisture and not over cook it
michelle
🙂
Diane Dilly
Frequently basting and cooking slowly keeps the turkey moist.
michelle
nice 🙂
claire toplis
basting and make sure you foil it
michelle
clever!
Mark Rayner
Bbasting and making sure that the oven is at the best temperature.
michelle
nice 🙂
Katrina Adams
Plenty of basting and making sure that the oven is at the best temperature.
michelle
Nice
Rebecca Atkins
I cook my turkey on a bed of carrots leeks and onions which keeps it moist. I the rub in butter salt and pepper few springs of thyme then cover in good quality streaky bacon
michelle
that turkey sounds really amazing
Tammy Neal
I cook mine with bacon on the top and covered in foil xx
michelle
Again, as I said, nice! 😉
Tammy Neal
I cook mine with bacon on the top and covered in foil xx
michelle
Nice!
joanne casey
I cover it in bacon, and cook slowly
michelle
Clever!
rhi
wrapped in bacon
michelle
yum! 🙂
Yvonne Sharpe
parma ham over the top covered in foil and pop in oven xx tasty
michelle
Nice!
Kay Broomfield
My husband puts bacon round the outside before roasting with some sticky maple glaze.
michelle
Sounds amazing!
sharon martin
roast is covered in foil to trap in the moisture, then take off for last half hour of so and sprinkle with salt to crisp up the skin
michelle
Clever 🙂
Dale Dow
okay I've only cooked turkey once and my method was stick it in the oven for the recommended time, this was mine and my husband's first Christmas but now we have kids and they don't eat turkey much so we try and use other meats, maybe we should try them with turkey for christmas, I miss it!
michelle
Go for it! Good luck Dale 🙂
kelly howells
Love your blog. Turkey instantly makes me think of Christmas!
michelle
Aw, thanks Kelly! 🙂
Jayne Kelsall
I cook mine covered in bacon and sausage and cook it really slowly wrapped in foil .x
michelle
Sounds amazing! I bet its really popular with the family :))
jennifer Hull
traditional roast.... basted in own juice.. served with all the trimmings..... bread sauce yummy
michelle
sounds delicious 🙂
Carole Nott
carefully apply oil and seasoning to the bird and cover with foil completely and slow roast
michelle
Nice!
Janet Birkin
My partner cooks it - always smells and tastes good, the turkey that is 🙂
michelle
Haha! Nice
misty
with lots of bacon!
michelle
Yes! 🙂
Lorraine Stone
We use extra butter for basting, herbs and salt and pepper. Cover with foil, then go for a crispy skin.
michelle
sounds delicious!
melanie stirling
We just cook it in the oven and then leave it to rest for a bit,it always tastes good.
michelle
Thanks for sharing Melanie 🙂
Jodi hill
I stuff with onions & carrots, then lay on a bed of root veg so the turkey isn’t touching the Tin, I pour over white wine, add some thyme & pop in the oven! Delicious
michelle
oooh, nice touch with the white wine. Haven't tried that before
Frances Sunshine Hopkins
I've never cooked one, my Mum does it
michelle
hehe, nice 🙂 Nothing better than a meal cooked by our Mums 🙂
laura banks
my hubby does it he pulls the skin back butter it salt and pepper and puts lemons and thyme in the cavity and it tastes yummy
michelle
clever! Great for extra flavors 🙂
Dean T
I just cover it with copious amounts of butter (under the skin) and bacon fat all over. Inside some sausage meat,fresh sage and onions. Old fashioned but you get a crispy skin and it never dries out
michelle
oh yes, butter is amazing for crispy skin 🙂
Jules eley
I put it in the oven and hope for the best!
michelle
Haha, when in doubt, I use a thermometer 🙂
vivian allman
i buy my turkey for Christmas day from the local farm butcher, all prepared and ready to cook, as it's the most magical meal of the year and i don't want anything to spoil it, so the best turkey from the best local farmer, makes sure it is.
michelle
clever! I might do that this year too if I run out of time 😛
Amy Pest
butter and thyme on the top stuffed with stuffing
michelle
Great combination Amy 🙂
Solange
Stuff with breadcrumbs, bacon, sausage, apple, raisins & dried cranberries and roast upside down.
michelle
Sounds delicious Solange 🙂
Lynda Graham
I stuff with lemon and sage, bacon on top.
michelle
sounds delicious
Elzbieta Znyk
My husband do it!
michelle
haha, clever 🙂 😉
TRACY JAMES
i cook my turey upaside down for a couple of hours ,then i turn it right way up ,place bacon on top of it and cook for the rest of the time
michelle
clever!
Sarah McVicar
I cook mine upside down then turn for the last 2 hours with streaky beacon on the top
michelle
Hi Sarah! Thanks for sharing. Great tip 🙂
Andrea Upton
I do different things each time, but I think covering the breast with bacon is nice
michelle
haha great idea 🙂
Kim Neville
I put some olive oil on the top of turkey and sprinkle some garlic salt and soya sauce
michelle
Thanks Kim, never tried using soy sauce!
Natalie Crossan
I stuff it with an onion and garlic, makes it just so scrummy
michelle
love onion and garlic. I also like to add some herbs with lemon 🙂
sam macaree
i get my mum to do it 😉
michelle
Nice! 🙂